此项目很久之前实践的项目,时间虽然过去了很久,但是近期将其整理出来,记录这个过程。
项目背景和挖掘目标
某市作为改革开放城市,经济发展在全国的经济中有着重要的意义,目前该城市在财政收入规模、结构等方面与北京、上海和深圳有一定的差距,存在不断完善的空间。本案例通过研究,发现影响该市目前以及未来地方财政建设的因素,并对其进行深入分析,提出对该市的地方财政优化和具体建议。
本次数据挖掘建模目标如下:
- 梳理影响地方财政输入的关键特征,分析,识别影响地方财政收入的关键特征的选择模型
- 结合上述因素分析,对某市2015年的财政收入及各个类别收入进行预测
分析方法和过程
大多学者建立财政收入和各待定的影响因素之间的多元线性回归模型,运用最小二乘估计方法来估计回归模型的系数,通过系数检验它们之间的关系,这样的结果对数据的依赖程度很大,并且普通的最小二乘估计求得的解往往是局部最优解,通过后续的检验可能会失去应有的意义。通过利用Lasso方法,进行变量的选择。通过变量选择的基础上,鉴于灰色预测对小数据量数据预测的优良性能,对单个选定的影响因素建立灰度预测模型,得出预测值。由于神经网络较强的适用性和容错能力,对历史数据建立训练模型,将灰度预测的数据结果带入训练好的模型中,充分考虑历史信息的预测结果。
数据探索分析
原始数据机构如下:利用excel表格存储相应数据。其中表头说明如下:时间从1994-2013
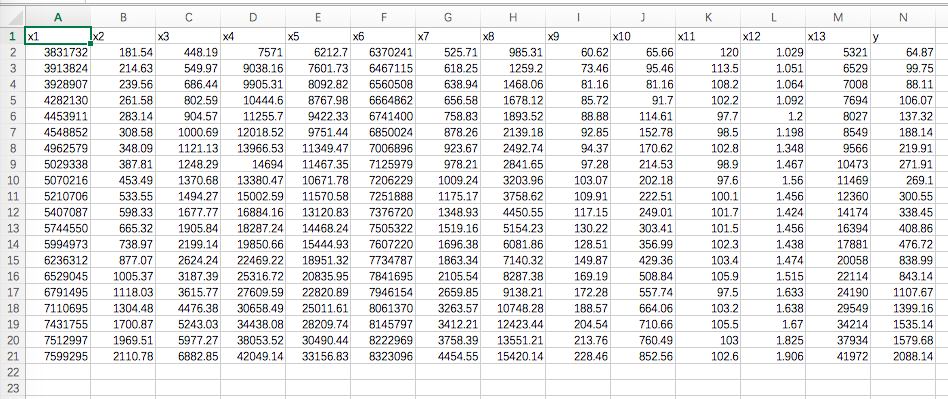
- x1:社会从业人数
- x2:在岗职工工资总数
- x3:社会消费品零售总额
- x4:城镇居民人均可支配收入
- x5:城镇居民人均消费性支出
- x6:年末总人口
- x7:全社会固定资产投资额
- x8:地区生产总值
- x9:第一产业总值
- x10:税收
- x11:居民消费价格指数
- x12:第三产业与第二产业产值比
- x13:居民消费水平
- y:财政收入
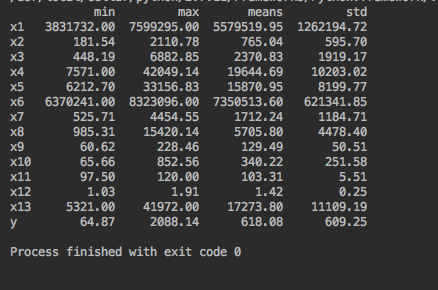
首先根据提供的基础数据分析,对数据整体有一个充分的认识,便于后续的数据分析工作和模型建立。利用,下属代码,分析数据的基础结构。
import numpy as np
import pandas as pd
inputfile = ‘数据文件路径’
data = pd.read_csv(inputfile)
r1 = [data.min(),data.max(),data.mean(),data.std()]
r1 = pd.DataFrame(r1,index=['min','max','means','std']).T
r1=np.round(r1,2)
print r1
结果如下:
分析完基础的数据,将数据概括后,我们开始研究定量与变量之间的关系,通过相关系数,判断因变量和解释变量之间是否有线性相关性。利用Person系数分析,具体代码如下:
import numpy as np
import pandas as pd
inputfile = '数据路径'
data = pd.read_csv(inputfile)
data = data.corr(method='pearson',min_periods=1)
data = np.round(data,2)
print data
模型构建
通过利用Adaptive-Lasso变量选择模型,对变量选择方法识别的影响财政收入的因素建立灰色预测和神经网络的组合预测模型,具体的灰度预测代码函数,可以看上一篇的blog,上边将灰度预测的算法利用python实现。具体的神经网络代码如下:
import pandas as pd
import tensorflow as tf
inputfile = '路径'
outputfile = '/Users/mac/Desktop/kk.xls'
#modelfile = './my_model_weights.h5'
data = pd.read_excel(inputfile) #读取数据
feature = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7'] #特征所在列
data_train = data.loc[range(1994,2014)].copy() #取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std #数据标准化
x_train = data_train[feature].as_matrix() #特征数据
y_train = data_train['y'].as_matrix() #标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() #建立模型
model.add(Dense(12, input_dim=6)) Dense,必须指定输入的变量和隐含层节点个数。
model.add(Activation('relu')) #用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(1, input_dim=12))
model.compile(loss='mean_squared_error', optimizer='adam') #编译模型
model.fit(x_train, y_train, nb_epoch = 1000, batch_size = 16) #训练模型,学习一万次
#model.save_weights(modelfile) #保存模型参数
#预测,并还原结果。
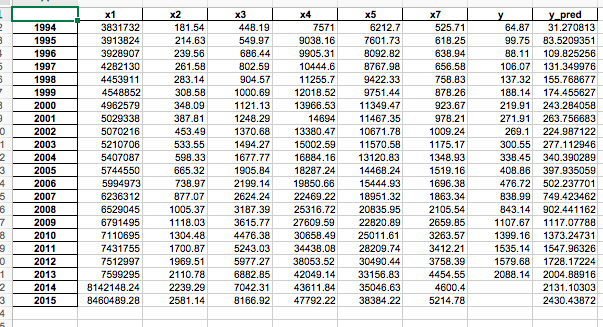
x = ((data[feature] - data_mean[feature])/data_std[feature]).as_matrix()
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data.to_excel(outputfile,encoding='utf-8')
import matplotlib as plt #画出预测结果图
p = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'])
plt.show()
微信支付
支付宝
