Merkle Patricia Tree简介
Merkle Patricia Tree是一种经过改良的数据结构，其融合了默克尔树和前缀树两种树的结构优点，在以太坊中用来组织管理账户数据、生成交易集合哈希的重要数据。 MPT树具有一下几个作用：
- 存储任意长度的Key－value键值对数据；
- 提供一种快速计算所维护数据集哈希标识的机制；
- 提供快速状态回滚的机制；
- 提供一种称为默克尔证明的证明方法，进行轻节点扩展，实现简单支付验证；
默克尔树
Merkle树是由计算机科学家Ralph Merkle在很多年前提出并由此命名，在比特币的网络中通过Merkle验证数据的正确性。在比特币的网络中，Merkle被用来归纳一个区块中的交易，同时生成整个交易集合的数字指纹。由于Merkle的存在，将比特币这种公链的产物，扩展为轻节点，使支付验证更加简单。
原理
在比特币网络中，merkle从下向上构建。在如下的例子中，首先将L1-L4四个单元数据哈希化，然后将哈希值存储到相应的叶子节点中，这些节点是Hash0－0，Hash0-1，Hash1-0，Hash1-1，通过合并相邻的两个哈希值，形成新的字符串，重复此步骤到根节点。
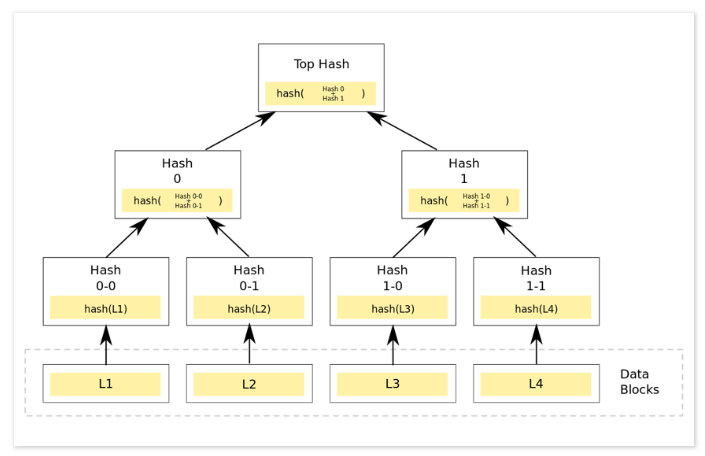具体根节点的计算可参考以太坊Merkle博客，上图中的一颗有着四个叶子节点的树，计算代表整个树的哈希需要7次计算，如果采用将这四个节点拼接到一起，只需要计算一次hash。但是为什么使用Merkle？
特点
- Merkle是一种树结构，可以是二叉树、多叉树，无论几叉树，都具有数结构的特点。
- Merkle树叶子节点的value是数据项的内容，或者是数据项的哈希值
- 非叶子节点的value是根据孩子的信息，通过hash算法计算得出
优势
- 快速重哈希
当Merkle节点发生变化的时候，只需要在当前发生变化的节点上计算，把跟发生变化的节点相关的节点再计算一次，便能得到新的根节点哈希值。
劣势
- 轻节点扩展
采用Merkle，只需存储区块头数据，不需要存储整个交易列表，回值列表等数据。
前缀树
前缀树（又称为字典树），用于保存关联数组，其键（key）的内容通常为字符串。前缀树节点在树中的位置是由其键的内容所决定的，即前缀树的key值被编码在根节点到该节点的路径中。如图所示：图中有六个叶子节点，其key值分别为to,tea,ted,ten,inn,A
<div align=center>
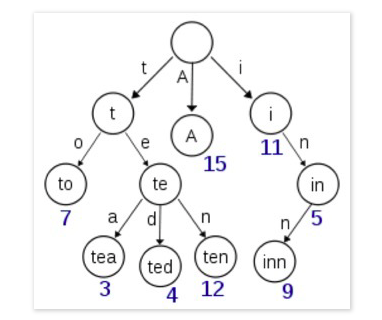
优势
相对于哈希表，使用前缀树来进行查询拥有共同前缀key的数据时十分高效，例如在字典中查找前缀为pre的单词，对于哈希表而言，需要遍历整个表，时间效率为O(n)；对于前缀树，只需要在树中找到pre的几点，且遍历这个根节点的子树即可。相对于前缀树，不存在哈西冲突问题。
劣势
- 直接查找效率低下
前缀树查找效率为O(m)，m为所查节电的key长度，而哈希表的查找效率为O(1)。且一次查找会有M次IO开销，相比于直接查找，无论速度还是对磁盘的压力都比较大。
- 可能会造成空间浪费
当存在一个节点，其key值的内容比较长，当树中没有与之对应的前缀分支时，为了存储该节点，需要创建许多非叶子节点来存储路径，造成存储空间浪费。
MPT结构设计
通过上述部分，前缀树可以通过key－value维护，但是其具有明显的局限性。无论是查询操作，还是对应数据的增删改查，效率低下，浪费存储空间。所以在以太坊中，为MPT新增不同的类型的树节点，压缩书的高度，降低复杂度。
MPT树中可以将树节点分为以下四类：
- 空节点
- 分支节点
- 叶子节点
- 扩展节点
分支节点
分支节点用来表示MPT树中多有拥有超过1个孩子节点以上的非叶子节点，其定义如下：
type fullNode struct {
Children [17]node // Actual trie node data to encode/decode (needs custom encoder)
flags nodeFlag
}
// nodeFlag contains caching-related metadata about a node.
type nodeFlag struct {
hash hashNode // cached hash of the node (may be nil)
gen uint16 // cache generation counter
dirty bool // whether the node has changes that must be written to the database
}
与前缀树相同，MPT同样是把Key－value数据项的key编码在树的路径中，但是key的每一个字节值的范围太大（［0-127］），因此在以太坊中，操作树之前，利用key编码的转换，将一个子节点高低四位内容分拆成两个字节存储。编码转换后，key‘的每一位的值范围都在［0，15］内。因此，一个分支节点的孩子至多只有16个。以太坊通过此方式，减少每个分支节点的容量，但实在一定程度上增加了树高。 分支节点的孩子列表中，最后一个元素是用来存储自身的内容。此外，每个分支节点会有一个附带的字段nodeFlag，记录一些辅助数据：
- 节点哈希：若该字段不为空，则当需要进行哈希计算时，可以跳过计算过程而直接使用上次计算的结果（当节点变脏时，该字段置空）
- 脏标志：当节点被修改时，该标志被置为1
- 诞生标志：当该节点第一次被载入内存中（或被修改时），会被赋予一个计数值作为诞生标志，该标志会被作为节点驱逐的依据，清除内存中“old”节点，节省内存资源。
叶节点&&扩展节点
叶子节点和扩展节点的定义相似，如下所示： ```go type shortNode struct { Key []byte Val node flags nodeFlag }
- key：用来存储属于该节点范围的Key
- val：用来存储该节点的内容
其中key是MPT树实现树高压缩的关键，在本文开头部分，提到前缀树会影响内存的使用，严重浪费内存存储空间。
微信支付
支付宝
